POOL SHAPES AND SIZES
It is essential to know how much water a pool holds. Though dose rates of pool chemicals do not have to be accurate down to the last gram or millilitre, they must be realistically close to the recommended levels.
It is not uncommon for pool owners to underestimate the amount of water in a pool, continuously under-dose, and then wonder why they have trouble.
Calculating pool volume is simply done, using the following equations.
Rectangular or square pools
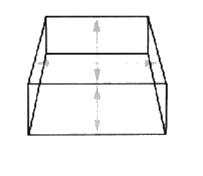Multiply length (metres) x width (metres) x average depth (metres) x 1000 = litres.
Circular pools
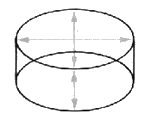Multiply the diameter (metres) x diameter (metres) x depth (metres) x 0.79 x 1000 = litres.
Oval pools
Multiply the long diameter (metres) x short diameter (metres) x average depth (metres) x 0.79 x 1000 = litres.
Kidney-shaped or other irregularly shapes pools
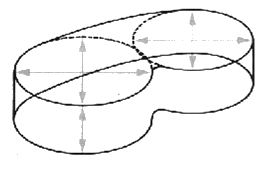Unusual pools can often be broken down into basic shapes for purposes of calculation. For example, a kidney shaped pool is roughly two circles joined together. Calculate the volume of the circles and add on about 10% to cover the area not included in the calculation. It is better to overestimate a pool volume than underestimate it
Note : Average depth is calculated by measuring depth at the deep end and at the shallow end, adding the figures together and dividing by two.
A guide to common pool volumes
| Circular Pools (metres) Diam x Diam x Av. Depth x 0.79 x 1000 |
Volume (Litres)* |
| 3.6 x 3.6 x 0.9 x 0.79 | 9 200 |
| 4.5 x 4.5 x 1.2 x 0.79 | 19 200 |
| 6.0 x 6.0 x 1.2 x 0.79 | 34 200 |
| 7.5 x 7.5 x 1.2 x 0.79 | 53 300 |
| 9.0 x 9.0 x 1.2 x 0.79 | 76 800 |
| Rectangular Pools (metres) Length x width, x Av. Depth x 1000 |
|
| 7.2 x 3.6 x 1.2 | 31 100 |
| 9.0 x 4.5 x 1.2 | 48 600 |
| 9.0 x 4.5 x 1.5 | 60 800 |
| 10.0 x 5.0 x 1.5 | 75 000 |
| 9.5 x 4.75 x 1.8 | 81 200 |
Dimensions (litres)*
Rounded figures*